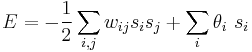Hopfield network
A Hopfield network is a form of recurrent artificial neural network invented by John Hopfield. Hopfield nets serve as content-addressable memory systems with binary threshold units. They are guaranteed to converge to a local minimum, but convergence to one of the stored patterns is not guaranteed. Furthermore, Hopfield networks provide a model for understanding human memory.
Contents |
Structure
The units in Hopfield nets are binary threshold units, i.e. the units only take on two different values for their states and the value is determined by whether or not the units' input exceeds their threshold. Hopfield nets can either have units that take on values of 1 or -1, or units that take on values of 1 or 0. So, the two possible definitions for unit i's activation, 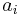 , are:
, are:
(1) 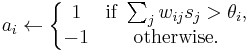
(2) 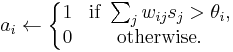
Where:
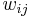 is the strength of the connection weight from unit j to unit i (the weight of the connection).
is the strength of the connection weight from unit j to unit i (the weight of the connection).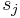 is the state of unit j.
is the state of unit j.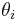 is the threshold of unit i.
is the threshold of unit i.
The connections in a Hopfield net typically have the following restrictions:
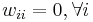 (no unit has a connection with itself)
(no unit has a connection with itself)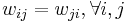 (connections are symmetric)
(connections are symmetric)
The requirement that weights be symmetric is typically used, as it will guarantee that the energy function decreases monotonically while following the activation rules, and the network may exhibit some periodic or chaotic behaviour if non-symmetric weights are used. However, Hopfield found that this chaotic behaviour is confined to relatively small parts of the phase space, and does not impair the network's ability to act as a content-addressable associative memory system.
Hopfield nets have a scalar value associated with each state of the network referred to as the "energy", E, of the network, where:
This value is called the "energy" because the definition ensures that if units are randomly chosen to update their activations the network will converge to states which are local minima in the energy function (which is considered to be a Lyapunov function). Thus, if a state is a local minimum in the energy function it is a stable state for the network. Note that this energy function belongs to a general class of models in physics, under the name of Ising models; these in turn are a special case of Markov networks, since the associated probability measure, the Gibbs measure, has the Markov property.
Human memory
The Hopfield model accounts for associative memory, through the incorporation of memory vectors. Memory vectors can be slightly used, and this would spark the retrieval of the most similar vector in the network. However, we will find out that due to this process, intrusions can occur. In associative memory for the Hopfield network, there are two types of operations: auto-association and hetero-association. The first being when a vector is associated with itself, and the latter being when two different vectors are associated in storage. Furthermore, both types of operations are possible to store within a single memory matrix, but only if that given representation matrix is not one or the other of the operations, but rather the combination (auto-associative and hetero-associative) of the two. It is important to note that Hopfield’s network model utilizes the same learning rule as Hebb’s (1949) learning rule, which basically tried to show that learning occurs as a result of the strengthening of the weights by when activity is occurring.
Rizzuto and Kahana (2001) were able to show that the neural network model can account for repetition on recall accuracy by incorporating a probabilistic-learning algorithm. During the retrieval process, no learning occurs. As a result, the weights of the network remains fixed, showing that the model is able to switch from a learning stage to a recall stage. By adding contextual drift we are able to show the rapid forgetting that occurs in a Hopfield model during a cued-recall task. The entire network contributes to the change in the activation of any single node.
The Network capacity of the Hopfield network model is determined by neuron amounts and connections within a given network. Therefore, the number of memories that are able to be stored are dependent on neurons and connections. Furthermore, it was shown that the recall accuracy between vectors and nodes was .138 (approximately 138 vectors can be recalled from storage for every 1000 nodes) (Hertz et al., 1991). Therefore, it is evident that many mistakes will occur if you try to store a large number of vectors. When the Hopfield model does not recall the right pattern, it is possible that an intrusion has taken place, since semantically related items tend to confuse the individual, and recollection of the wrong pattern occurs. Therefore, the Hopfield network model is shown to confuse one stored item with that of another upon retrieval. But this can be improved before applying the dynamical rule (which is explained in the next paragraph) and adding some noise to the activations.
McCullough and Pitts (1943), dynamical rule, which describes the behavior of neurons, does so in a way that shows how the activations of multiple neurons map onto the activation of a new neuron’s firing rate, and how the weights of the neurons strengthen the synaptic connections between the new activated neuron (and those that activated it). Hopfield would use McCullough and Pitts, dynamical rule, in order to show how retrieval is possible in the Hopfield network. However, it is important to note that Hopfield would do so in a repetitious fashion. Hopfield would use a nonlinear activation function, instead of using a linear function. This would therefore create the Hopfield dynamical rule and with this, Hopfield was able to show that with the nonlinear activation function, the dynamical rule will always modify the values of the state vector in the direction of one of the stored patterns.
Running
At each step, pick a node at random. The node's behavior is then deterministic: it moves to a state to minimize the energy of itself and its neighbors. (In contrast, the Boltzmann machine has a stochastic update rule.)
Training
Training a Hopfield net involves lowering the energy of states that the net should "remember". This allows the net to serve as a content addressable memory system, that is to say, the network will converge to a "remembered" state if it is given only part of the state. The net can be used to recover from a distorted input the trained state that is most similar to that input. This is called associative memory because it recovers memories on the basis of similarity. For example, if we train a Hopfield net with five units so that the state (1, 0, 1, 0, 1) is an energy minimum, and we give the network the state (1, 0, 0, 0, 1) it will converge to (1, 0, 1, 0, 1). Thus, the network is properly trained when the energy of states which the network should remember are local minima.
See also
- Associative memory
- Autoassociative memory
- Boltzmann machine — like a Hopfield net but uses annealed Gibbs sampling instead of gradient descent
- Ising model
- Hebbian theory
References
J. J. Hopfield, "Neural networks and physical systems with emergent collective computational abilities", Proceedings of the National Academy of Sciences of the USA, vol. 79 no. 8 pp. 2554–2558, April 1982.
Hebb, D.O. (1949). Organization of behavior. New York: Wiley
Hertz, J., Krogh, A., & Palmer, R.G. (1991). Introduction to the theory of neural computation. Redwood City, CA: Addison-Wesley.
McCullough, W.S., & Pitts, W.H. (1943). A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics,5, 115-133
Polyn, S.M., & Kahana, M.J. (2008). Memory search and the neural representation of context. Trends in Cognitive Sciences, 12, 24-30.
Rizzuto, D.S., & Kahana, M.J. (2001). An autoassociative neural network model of paired-associate learning. Neural Computation, 13, 2075-2092.
External links
- Chapter 13 The Hopfield model of Neural Networks - A Systematic Introduction by Raul Rojas (ISBN 978-3-540-60505-8)
- Hopfield Neural Network Applet
- Hopfield Neural Network implementation in Ruby (AI4R)
- The Travelling Salesman Problem - Hopfield Neural Network JAVA Applet
- scholarpedia.org- Hopfield network - Article on Hopfield Networks by John Hopfield
- Hopfield Network Learning Using Deterministic Latent Variables - Tutorial by Tristan Fletcher
- Neural Lab Graphical Interface - Hopfield Neural Network graphical interface (Python & gtk)